Computersimulation eines Tesla-Transformators

Die Ausgangsgrösse für die Simulation bildet die elektrische Ladung Q. Um die

Bewegung der elektrischen Ladung im System beschreiben zu können, werden

hier die einzelnen, über den Bauteilen der Anlage liegenden elektrischen

Spannungen betrachtet. Der Aufbau der Anlage ist in Fig.1 gezeigt.

Fig.1. Aufbau eines Teslatransformators: Die Primärspule ist durch die Induktivität L₁

und die Sekundärspule durch L₂ bezeichnet, C₁ ist die Kapazität des Kondensators

im Primärkreis und R= R(t) stellt den elektrischen Widerstand dar,

welcher vor allem mit der Funkenstrecke assoziiert ist.

Es wird hier von einer Anlage ausgegangen, welche mittels eines Netzfrequenz-

Transformators (50 Hz) versorgt wird. Dieser lädt den Kondensator auf einen

bestimmten Wert auf. Bevor die Spitzenspannung (ca. 15 - 18 kV) überschritten wird,

zündet die Funkenstrecke und der Kondensator entlädt sich blitzartig,

welche mit einer entsprechend schnellen Änderung des Stromflusses durch

die Primärspule des Tesla-Transformators verbunden ist. Damit ändert sich auch

das magnetische Feld, welches die Sekundärspule durchfliesst. Somit wird in der

Sekundärspule eine elektrische Spannung induziert. Die Höhe dieser Spannung

lässt sich durch die Werte der Kapazitäten im Primär- und Sekundärstromkreis abschätzen.

Dabei wird die im Kondensator des Primärkreises gespeicherte Energie betrachtet.

Diese ist gegeben durch die Kapazität C₁ und die

anliegende Spannung U₁: . Die Kapazität des Sekundärschwingkreises

ist gegeben durch die Konduktorkugel oder den Torus, welcher am Ende der Sekundärspule

angebracht wird, sowie die Kapazität der Sekundärspule selbst (welche durch die Oberfläche

des Drahtes und somit durch dessen Durchmesser und die Anzahl Windungen bestimmt wird).

Wird von einer verlustfreien Energieübertragung ausgegangen, dann gilt für das Verhältnis der

Spannung U₁ im Primärkreis zur Sekundärspannung U₂:

Hohe Sekundärspannungen können demnach durch kleine Sekundärkapazitäten und grosse

Primärkapazitäten erreicht werden. Jedoch beeinflussen die Kapazitäten das Verhalten der

Ladungen in den beiden Stromkreisen grundsätzlich, was klar wird, wenn die elektrischen

Spannungen über den einzelnen Komponenten betrachtet werden. Dies soll zuerst am isolierten,

d.h. nicht mit dem Sekundärstromkreis gekoppelten Primärstromkreis erläutert werden. Bei

leitender Funkenstrecke (mit dem elektrischen Widerstand R₁) kann mit Benützung der

Maschenregel (Kirchhoffsche Gesetze) für die Summe der Spannungen U_k im

Primärstromkreis geschrieben werden:

Dabei ist U_C die Spannung über dem Kondensator, U_L die Spannung über der Induktivität L₁

und U_R die Spannung über der Funkenstrecke. Mit der im Kondensator des Primärkreises

gespeicherten elektrischen Ladung Q₁ = C₁U, dem Ohmschen Gesetz U_R = R₁I₁ und dem

Induktionsgesetz resultiert:

Die Ladung Q₁ = Q₁(t) ist eine zeitabhängige Funktion. Genau genommen handelt es sich um

die Ladung auf einer Seite des Kondensators. Der Zusammenhang zum Stromfluss ergibt sich

durch I₁ = dQ₁ / dt. Durch ersetzen von allen Strömen in Eq.2 ergibt sich

folgende Differentialgleichung:

Die Differentialgleichung kann durch folgenden Ansatz gelöst werden: .

Dabei ist die maximale elektrische Ladung auf einer Seite des Kondensators und φ ist

eine allgemeine Phasenverschiebung. Die Ladung Pendelt also mit der Kreisfrequenz w

hin und her, es handelt sich um einen gedämpften elektrischen Schwingkreis. Durch Einsetzen

des Ansatzes kann der Dämpfungskoeffizient l und die Kreisfrequenz w bestimmt werden.

Für die Dämpfung resultiert:

Die Kreisfrequenz w kann aus L₁ und C₁ berechnet werden:

Die analytische Lösung liefert bereits die Information über das grundsätzliche Verhalten des

Primärstromkreises. Zündet der Funke über der Primärfunkenstrecke, so wird das System zu

Schwingungen angeregt. Bei Teslatransformatoren liegen die Frequenzen im Bereich von

50 – 500 kHz. Es handelt sich also um Hochfrequenzschwingungen. Im Vergleich dazu erfolgt

das Zünden der Funkenstrecke nur 100-mal pro Sekunde, wenn das System mit einem

Netztransformator versorgt wird. Je nach Funkenstrecke wird aber der Strom nicht einfach

ein- und ausgeschaltet. Die genauen Prozesse an der Funkenstrecke sind noch recht

unbekannt und schwierig zu simulieren. Der Einfluss der zeitlichen Entwicklung

des Widerstandes R(t) der Funkenstrecke auf das System kann mittels

Computersimulation untersucht werden.

Zentral für die Simulation des Tesla-Transformators ist die Übertragung der Schwingungen

vom Primär- auf den Sekundärkreis und die Rückkopplung zwischen den beiden Stromkreisen.

Im Prinzip handelt es sich um zwei gekoppelte Schwingkreise mit der Kopplungskonstante

M / L_i. Zur Gleichung Eq.4 muss nun eine zweite Systemgleichung hinzugefügt werden,

welche den zweiten Schwingkreis beschreibt:

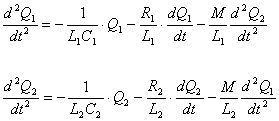
Für die Simulation des isolierten Primärstromkreises wird in diesem Projekt die Simulationssoftware

Vensim verwendet. Für die Implementierung wird die Differentialgleichung in zwei

Differentialgleichungen erster Ordnung zerlegt:

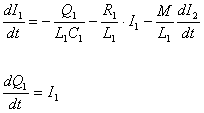
Für den Sekundärstromkreis ergeben sich die analogen Gleichungen durch Vertauschen der Indizes.

Die elektrische Spannung über dem Kondensator ergibt sich für den Primärkreis aus .

Die Spitzenspannung beträgt dabei bei den meisten Tesla-Anlagen ca. 12 – 18 kV.

In Analogie dazu lässt sich die Spannung im Sekundärkreis aus Q₂ und C₂ berechnen.

In Vensim können (wie in vielen anderen Systemdynamikprogrammen) die Systemgleichungen

graphisch programmiert werden (Scheidegger, S. (2008): Computersimulation eines Tesla-Transformators.

VSMP-Bulletin 107, 2008; 10-17)

Zur Verifikation des Modells wurden die Messungen und Simulationen von Denicolai verwendet

[Denicolai, M. (2001): Tesla Transformer for Experimentation and Research. Licentiate Thesis, 2001,

Helsinki University of Technology]. Denicolai verwendete einen Tesla-Transformator mittlerer Grösse,

dessen Sekundärspannung bei 350 kV liegt. Für die Verifikation wurden die Parameter,

welche Denicolai für seine Simulation verwendete eingegeben (Tab2).

Tab.2. Parameter für den Vergleich der Simulationen.

Parameter	Werte
Primärspannung U1	11.5 kV
Widerstand R1	1.05 W
Primärkapazität C1	96.7 nF
Primärinduktivität L1	65 mH
Kopplung M	528.05 mH
Kapazität C2	74.4 pF
Induktivität L2	76.98 mH
Widerstand R2	100 W

Die Simulation mit dem Modell in Fig.2 ergab im unbelasteten Zustand die gleiche Spitzenspannung

von 350 kV bei gleicher Frequenz im Sekundärschwingkreis (68 kHz). Dies gilt sowohl für den

Vergleich mit den Simulationswerten von Denicolai, als auch für den Vergleich mit den realen

Messwerten an der Anlage.

Bei der Anlage von Denicolai lässt sich der Kopplungsfaktor durch Verändern der Primärspulenposition

variieren. In Fig.2 ist der zeitliche Verlauf der Sekundärspannung U₂(t) für M = 423.05 mH gezeigt.

Die Schwingungsbäuche zeigen, wie die Energie zwischen Primär- und Sekundärkreis hin- und herpendelt.

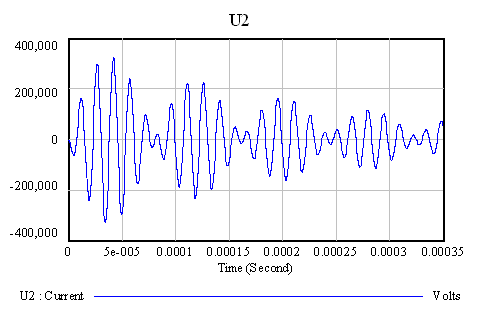
Fig.2. Zeitlicher Verlauf der Sekundärspannung U(t) in der Vergleichssimulation. Numerik:

Runge-Kutta-Verfahren, Dt = 1·10^-9 s